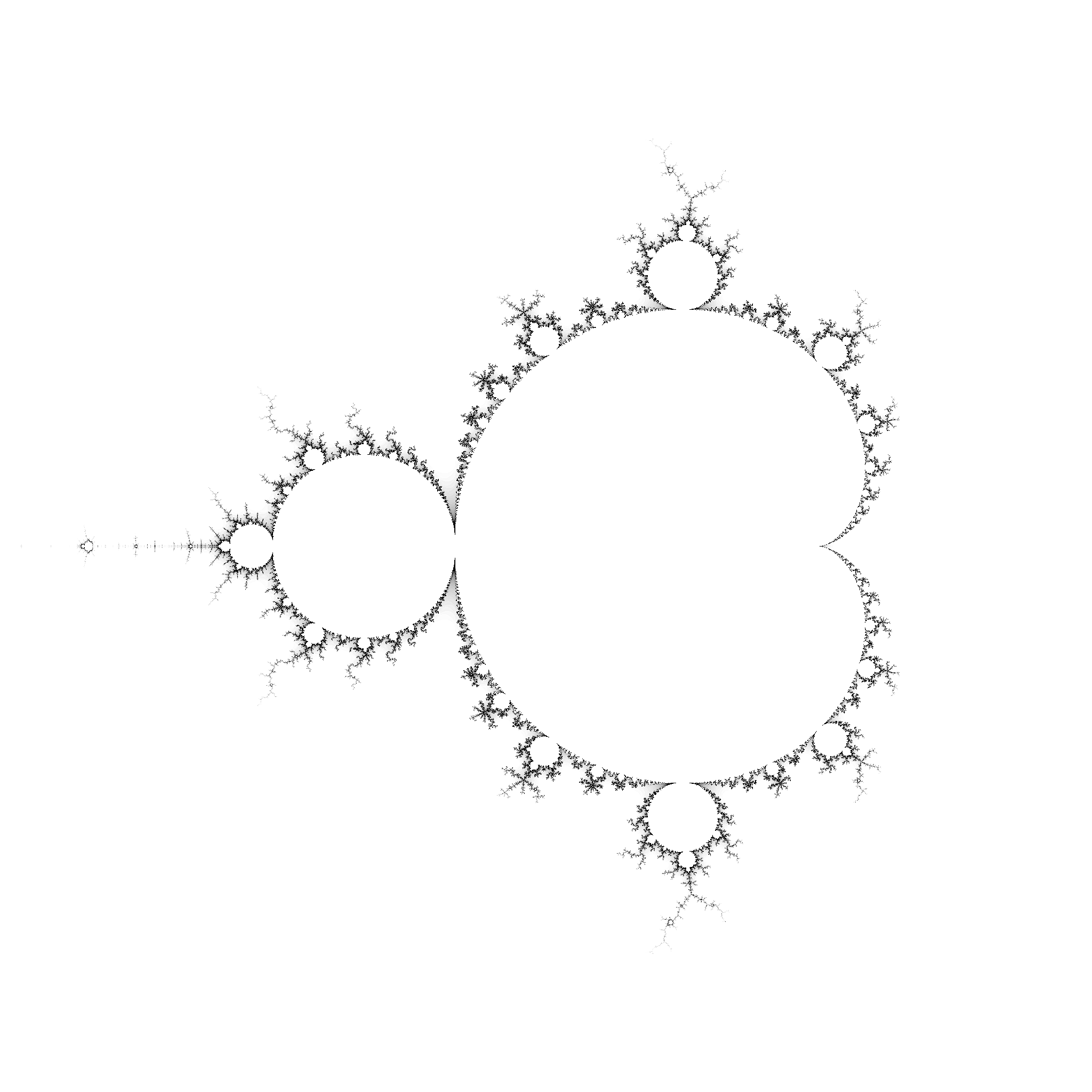
Analysis of a model of n-dimensional representations of the Mandelbrot set, exploration of particular fractal forms in architecture.
Foreword
The aim of this essay is to show that there are parametric design tools that would make it possible to create and develop architectural thinking that takes into account balance and harmony in the relationships between the scales of perception of a project in the city. It should raise awareness of the omnipresence of fractals in our environment as well as in architecture for millennia. The reader should understand that fractals are not a solution for contemporary architecture but a tool.
“A tool makes it possible (but not necessary) to carry out a task or a set of tasks, a tool makes it possible (but not necessary) to take action. While the possible opens up other possibilities (to creation), the cause leads to an effect or a set of effects, and only one. This being said, in the absence of a tool it may be impossible to perform a certain action. The true creative process consists in diverting the conventional use of a tool, giving it another meaning, notably by attributing another function to it. This is exactly how invention occurs in architecture, giving rise to a new concept.” 1
The fractal tool has the interest of being accessible to all and intellectually conducive to discovery and fascination in all fields, artistic, mathematical, medical. It is also a kind of universal language between all these fields. We are only now beginning to understand how animate and inanimate matter is organized in a complex way to form a coherent whole. The results of quantum physics, complexity theory, systems analysis, artificial intelligence, and fractal geometry converge to give us a much more complex view of the universe and life.
Fractals are a powerful intellectual development tool that goes beyond physics; the theories of order and chaos, the theories on the fractal dimension of the universe are all sources of inspiration and passion. This dissertation is addressed to the reader with the aim of sharing a passion, a moment of escape but above all the possibility of travelling in unknown dimensions at the frontier of the perceptible.
Two points of presentation should be pointed out. To avoid interrupting the continuity of the text, figures and illustrations are grouped together at the beginning of the essay. To make them easy to find, they are denoted by the chapters they illustrate. The reader should be aware of the following concepts: algorithmic, parametric, fractal geometry, Euclidean geometry, fractal dimension, fractal scale. A lexicon and an appendix at the end of the book will enable the reader who wishes to find these notions or the definitions that he would not have yet. This essay is also presented as a collection, the texts in the appendices, and the underlying questions outlined, illustrate both the subject and the following presentation.
Introduction
“Architecture is no longer drawn, it is programmed, it is no longer shown, it is calculated. Perception and design are then disrupted. These new tools are rooted in a deconstructivist conception, where the explosion of form leads to generative processes characteristic of an algorithmic architecture. The aim is then to deconstruct the usual building design codes at all levels”.2
In this context, the approach of architectural design using computer software, and particularly algorithms, produces forms. These forms are not architecture. Architecture is a sensible articulation between solidity (firmitas), utility (commmoditas) and beauty (venustas). We must therefore be careful not to be satisfied with the mirages of the spectacular.3
Therefore, this essay will seek to explain how fractal parameterization can be understood, defined and used as an architectural code as well as a design tool. Based on the Mandelbrot set and its three-dimensional geometric representation the Mandelbulb, how to produce an architectural code, how to use this code to design a project?
Observed globally and in its local characteristics, how can one, using an emblematic representation of fractals, i.e. the n-dimensional representation of the Mandelbrot complex, attempt to extend a creating model to higher dimensions?
Thus the problem would be stated as follows:
Analysis of a model of n-dimensional representations of the Mandelbrot set, exploration of particular fractal forms in architecture.
1 Introduction to fractals
1-1 Presentation of fractals
The purpose of this brief presentation of fractals is not to recopy for the nth time definitions that are much more provided, but simply and firstly to show that fractals are a universal tool within everyone’s reach to understand the world around us. I highly recommend to the curious reader the book “Fractal objects, random shapes and dimensions” by Benoit Mandelbrot.
Each of us has notions about the meaning of the term fractal, some will say that it is a geometric form with particular properties, others that it is a length that cannot be calculated, and finally, everyone knows something about fractals for the simple reason that we encounter them every day around us. It is therefore by observing what surrounds us that I propose to approach fractals. The veins of a tree leaf, a river seen from the sky, lightning, some shells, (I suggest you watch the Arte documentaries on fractals which are very rich in information but above all images which often speak much better than a speech or a long demonstration.) All have particular geometrical characteristics and more particularly scale symmetries, i.e. we can look closer and even closer we will always find similarities and patterns that repeat themselves. The complex shapes of living species are in fact almost always the result of basic equations, very simple, repeated ad infinitum. Where the result of the equation is injected back into the terms and recalculated many times, this is called iteration (from the Latin verb iterare meaning “to walk” or to iter, “the way”) and refers to the action of repeating a process. This is the very principle of fractals.
It should be noted that a fractal object in nature is self-similar only on a certain range of scales. A fractal in mathematics, on the other hand, is similar indefinitely. Because in mathematics, we are interested in dynamic systems acting on mathematical quantities, and not on physical quantities. Typically, numbers. The rule for moving from one number to the next is a formula. The iterative calculation, allows the application to recursive equations, which is used systematically today in algorithmics. Fractals are invariant figures by scaling (we also speak of “auto similar structures”) and are the graphical representation of contracting recursive sequences (for the “systems of deterministic iterated functions” that we will see later) or non-divergent (for the escape-time fractals).
The fractal figures can be divided into three main categories:
“Natural fractals”, random fractals, generated by stochastic and non-deterministic processes. Random fractals are the most widely used in practice, and can be used to describe many extremely irregular real-world objects. Examples include clouds, mountains, fluid turbulence, coastlines, and trees. Fractal techniques have also been used in fractal image compression, as well as in many scientific disciplines.
“Fractal objects”, regular fractals. These have a fixed geometric rule of replacement (the Cantor set, the Sierpinski carpet, the Sierpinski triangle, the Peano curve, the Koch flake). form iterated systems of functions.
“Deterministic fractals”, fractals defined by a recurrence relation at each point in a space (such as the complex plane). Examples of this type are the Mandelbrot sets and the Lyapunov fractal;
Now that we have a quick but global view of fractals, let’s take a look at architecture.
1-1-1 Fractals in architecture
Geographers have been interested in fractal geometry for about forty years now, following the pioneering work of Benoît Mandelbrot4.
There are many themes in the application of fractals to architecture, but one area has been treated more than any other by fractalists: that of the city. Michael Batty and Paul Longley are without doubt the first authors who were interested in the applications of fractals in this field: as early as the mid-1980s, they began to study the fractality of urban structures in order to better simulate the growth of these organisms. 5 Pierre Frankhauser published a more general synthesis of what could be expected from fractal geometry in urban geography.
With the multiplication of geographic information systems in the fields of urban management and cadastre during the 1990s, it became possible to derive data from digital plans and to work on the fractality of urban morphologies at much larger scales.
In vernacular architecture, the process of fractal appearance is at the same time intuitive and involuntary. Indeed, man, inspired by the proportions and harmonious relationships of nature, simply copied what have been called natural fractals. Then, inspired by architecture itself, he created his own fractal geometries in the image of the Bukhara and Masharabiah in Islamic architecture. An example is the Abencerrages Hall. Long before the pyramids, the pyramids of Cheops are perhaps the first sign of fractal architecture, directly related to human nature and in the image of it, and are reminiscent of Sierpinsky’s famous triangle.
A little later in history, the Villas of Palladio, analyzed by Emmanuelle P. Jeanneret in her doctoral thesis7 , also abound in fractals. Generally speaking, classical architecture is bathed in fractal geometry8.
8 Gaudi, in designing La Sagrada Familia, took his inspiration from nature; the fractals (in elliptic/split facades) used for the design give it a special character. In an article by Francis Leguen, the name “Fractalia Familia” takes on its full meaning, but if the fractal dimension appears to us visibly today, how did Gaudi use these tools even before the “discovery” of the so-called fractals9.
Today, in his book “Les villes et les formes”, Serge Salat develops an approach using fractals in urban analysis. He explains in his book how fractals draw vernacular cities and how to recognize and analyze them. He also directed an art exhibition “Beyond the Vision in Beijing on September 24th 2011”. His work can be discovered on the Internet10 and focuses on conditioning in a fractal space11.
The reader will have understood how urbanism and architecture are permeated by fractals. Let us now come back to the third type of fractal, those which interest us more particularly: deterministic fractals.
1-1-2 Deterministic fractals
Deterministic fractals are based on iterated functions that are strictly self similar. The family of fractals so named by Michael Barnsley in 1987: the “deteministic iterated function systems” (IFS) Of all fractal figures, only those constructed using iterated function systems usually display the property of self-similarity, meaning that their complexity is invariant to change of scale. The best known is the Mandelbrot set.
1-2 Benoit Mandelbrot
A pioneer in the use of computers for visualization and experimentation in mathematics, Benoit Mandelbrot is the father of fractals.
“Benoit Mandelbrot was a visionary, and his vision was geometric. Of course the essence of this geometric vision is translated by the term he coined for fractal geometry. And fractal geometry is a mathematical field of which, before Benoît, certain flowers, singular trees and tasty fruits were well known, but in the wild, or cultivated in small gardens. It was Benoit who opened up the field by showing the extent of its applications and giving it a name. The creation of the word is inseparable from the concept, and Benoit had a kind of genius of language, to bring singular flowers to civilization”.12
1-2-1 The Mandelbrot Ensemble
We arrive at a point in the presentation where mathematics becomes necessary, and writing less digestible. The following definition is succinct and deserves to be completed by reading the very well written articles on Wikipedia about the sets of Mandelbrot, Julia and the mathematical spaces in which these sets evolve13. But it gives a first taste of the ensemble.
Let the suite Zn+1 = Zn2 + c with Z0 = 0 and c any complex number.
The question Mandelbrot asked himself is the following: According to the value of c, what behavior will the sequence have? Will it converge, diverge or be cyclic? The idea is to use a computer to scan a region of complex space. For each pixel of the screen a value of c is associated and the behaviour of the associated sequence is calculated. If a Zi has a module greater than 2, the sequence will diverge. We then draw the pixel of the color i. If, after a maximum number of iterations n, the modulus of Zn is always less than 2, the sequence is not considered to diverge.14( The set is bounded by [-2;1]). The Mandelbrot set is the boundary between the space where the sequence converges and the space where it diverges. It is visible by the distance bound estimator algorithm and gives a good idea of the nature of the set.
We notice that the Mandelbrot set is very complex. One even has the impression that it covers a surface. In fact, its “fractal dimension” is 2, and it includes all the subsets of Julia.15 If the Mandelbrot set is not self-similar in the sense that the shapes encountered betray the area of enlargement, we can still say that it is “formed from a multitude of copies of itself”. He is the basis of the theories of order and chaos. It is the symbol of a way of conceiving and perceiving the world.
1-2-2 Mandelbrot in architecture
Examples of the use of the Mandelbrot complex, applied to the study of architecture and urban planning, are illustrated by Serge Salat and Pierre Fankhauser, who used the Mandelbrot complex as a code in the study of cities.16
Until now, all studies have been two-dimensional; simply because the study of cities is done on such a large scale that it is only perceived with a certain hindsight. Also the fractal representation used until a few years ago was only a two-dimensional representation.
2 An n-dimensional model
2-1 In search of the Mandelbulb
However, since 2009, computer scientists (such as Daniel White and Paul Nylander) who are passionate about the fractal tool and the Mandelbrot set, have decided to represent the Mandelbrot set in a hypercomplex plane; and have found a model in an 8-dimensional plane, the quaternion (4-dimensional plane) not allowing to represent it correctly. The discovery of the Mandelbulb took almost thirty years of investigation, it is found in the work of Rudy Rucker in “In Search of a Beautiful3D Mandelbrot Set”, which explains the different methods that led to the creation and representation of the Mandelbulb and is in Appendix 2.
Thus, an n-dimensional representation of the sets derived from Mandelbrot, the Mandelbulb, was obtained. The Mandelbulb is the set of points in space that do not diverge after infinite iteration of a double folding transformation of space. It can be defined in any type of dimensions, although the 3D version is the most popular. A new door is opening, because although the existence of three-dimensional fractals and their study had been known for a long time, the possibility of parametrizing them to obtain a directly usable representation remained unsolved. Today, their work opens up a wide range of possibilities both in the analysis and now in the creation of architectural forms.
2-2 Mandelbulbs’ creation software
There are many fractal representation softwares and more particularly Mandelbulbs, among the best known I will quote Ultrafactal, Apophysis, Mandelbulb3D, Mandelbulber, Mandelx. I chose to use Mandelbulb 3D, you will find excellent tutorials on the Fractalforum website17, and I will develop its potential use in an appendix to be published (it represents almost a chapter by itself).
2-3 Results and Mandelbulbs exploration
In the manner of Emmanuelle P. Jeannneret’s work on Palladio, the Mandelbulb can be considered as a model. Emmanuelle P. Jeanneret explains how to decompose the model in order to extract a greater common descriptor. This one is used as an invariant, the basis to create variance (for 2D fractals, it corresponds to the initiator) thanks to the form grammar or rules (generator). The interest of Mandelbulbs, as we can see later with the Mandelbox, is that this invariant can itself be a fractal.
Let’s discover the infinite wealth of Mandelbulbs and Mandelboxes. This part is based on the work of Francis Leguen in his article “The Hidden Worlds of the Mandelbox18” and is illustrated with his text and images.
The Mandelbox is one of the famous three-dimensional fractals Discovered by Tom Lowe in 2010, it is defined in a similar way to the Mandelbulb. It is also called Amazing Box. It has become the darling of fractalists of all stripes. It must be said that this Pandora’s box contains all sorts of mysteries and exceptional visions. One of its remarkable properties is that it contains a lot of other “classic” fractals, as we will see.
In the Mandelbulb3D software, the default Mandelbox has nothing extraordinary. But the trick is to explore its negative dimensions, in particular the -1.5 dimension as represented on the “cube “19. Now, let’s zoom in on one of the corners. The first thing we notice is the self-similarity, characteristic of fractals: the cube pattern repeats itself indefinitely, at all scales20. But if we take a closer look, a well-known figure appears, that of the Apollonian fractals21.
Let’s zoom in again… Easily recognizable areas of some “classic” fractals appear. On the circumference of the cube appears a smooth part made of a Menger sponge. We also easily find the Koch flake, Poincaré’s disc and hyperbolic paving, Sierpinsky’s carpet, Cantor’s ensemble, IFS fractals and many others. I deliberately used the same lighting and colours so as to be able to compare the shapes well22. But these are not the only treasures hidden in the Mandelbox… Here are some “deeper” visions, inside the box but keeping the same dimension of -1.523.
Nothing prevents you from exploring the other negative dimensions, between -1.5 and -1.2 to discover other secrets. And of course to combine this basic figure with the other fractal solids available in the Mandelbulb 3D or Mandelbulber software. Bad news: the possibilities are endless.
Also the geometry of Mandelbrot seems very complete, since it allows to generate a wide range of shapes, and many natural and non-natural objects are derived from it. But it also makes it possible, and it is important to remember this, to write rules of financial grammar. In his latest book, Benoit Mandelbrot deals with the fractal tool applied to finance. If the same language allows us to predict stock market cracks as well as to produce urban morphologies, how can we not ask ourselves the question of the universality of the language, but also of the coherence of writing between the different domains that use it. The variants of society can be deciphered with the same code, the same alphabet, but the deterministic and stochastic rules make them two languages that get along with different declensions.
2-4 Retrieving and Using Information
I give you here an almost complete article by Francis Leguen because it is disconcertingly clear and traces the steps to be taken to extract the mandelbulbs from their pixelated case to have a model usable in architecture.
“Thus, we can now extract the fractals from their generative software. This was already possible with Incendia, Xenodream, ContextFree but we were eagerly awaiting the availability of this function on Mandelbulb3D. It’s done with version 1.7.6 where you can (in principle) export your creations in .obj format to use them elsewhere…The procedure is far from obvious and requires a (very) powerful machine.
The fractal landscapes that we generate with Mandelbulb3D are already 3D objects since we can navigate inside. In fact, it is the 3D projection of 4-dimensional spaces and even more. 3D projection itself projected in 2D on the computer screen… The challenge is to recover the fractal 3D space to make it a “real” 3D object that can be manipulated in other software. It is possible! The trick is called voxelization. It’s very simple: you just have to cut the volume into small orthogonal cubes, in order to obtain a “julienne of fractals”. The smaller the cubes, the more definition and detail is preserved in the solid. Ideally each cube should be the size of a pixel. It has become a pixol! Which is defined with spatial coordinates in 3 dimensions. In short, it is a 3D object whose resolution depends on the degree of “decimation”.
Until now, there were two tedious methods to achieve this. The first one, entirely in Mandelbulb3D, consists in using the animation module with the camera in top view and zooming (with the right settings) until crossing the Mandelbulb from one side to the other. As the animations are rendered as a collection of images (several thousands), all you have to do is enter these images into a software program capable of interpreting the sequence of images to make a 3D solid. There are several of these in the scientific and medical field (this is how brain scans are used, for example.) The other method consists of making a certain number of high definition renderings by modifying the point of view each time, so as to go around the object that you want to “voxelize”. These images are then entered into a software program that reconstructs the 3D object, taking into account the angle variations of each image. It’s quite magical. You can even use a software from the cloud: Autodesk 123D Catch (ex Photofly). All this works but at the price of pharaonic efforts… Hence the mystical enjoyment of fractalists of all hairs at the appearance of voxelization in Mandelbulb3D…
Let’s see what this new feature looks like. It can be accessed from the main window, tab Utilities/ VoxelStack. By clicking on the button “Import parameter from main” you should see your sliced fractal appear… You have to zoom out with the bottom button “Overall scale” to the values 0.6 otherwise the fractal will be truncated. Set the Z slices (by default to 100 but I went up to 900…) which determines the fineness and the definition of the final object (the smaller the cubes will be, the heavier the object will be…). Launch “Start rendering slices”: a few thousand images will stack up in the specified folder. We’re happy. And what do we do with these images, carefully numbered? We blow a big blow because we’re now going to use even more exotic software to process these images. There are two tools that are useful for this task. With different fortunes depending on the weight of the fractal … We can download ImageVis3D at the University of Utah … Or Fiji. In short, you can actually recover 3D objects that you can import in a lot of 3D pro or less pro software, like Carrara or even Bryce. It’s a technical satisfaction but in the end, we don’t find what makes the magic of 3D fractals: their infinite level of detail. And that’s where the problem lies: complex fractals result in objects of several gigas, practically unusable… Even Mac’s find themselves on their knees… And the details are not as “detailed” as in Mandelbulb3D. The ideal would be to be able to simplify (and thus lighten) the geometries to the extreme and then “tighten” them with a hypernurbs for example. Maybe this is possible with Meshlab…Anyway, it’s too late: the mandelbulbs have escaped from the box and we won’t go back…What uses for these new solids? Imagination in power! Exploration continues… “
And if mandelbulbs already existed…In a January 2013 article, Francis Leguen explores the possibility of discovering Neolithic mandelbulbs…24
3 Exploration and use in architecture
3-1 Fractal scale and architectural anthropocentrism
The relationship on a human scale is an essential theme. We must be able to relate to architecture by a fractal cascade of successive scales from details on our own scale. This means,” writes Pierre Riboulet, “in the first degree, very simply, that all the constructed elements that can be apprehended with the hand, with the body, must be calculated according to human dimensions. The height of a ceiling, the sill of a window, the step of a staircase, the width of a corridor or a pavement must be dimensioned in such a way that, through the use made of them, one immediately feels an adequacy between these spaces and one’s own body. »
From Riboulet always, “Discovering the right scale is always a necessary thing in composition work. It has to be established for the fragment that one is composing, and this scale has to be in harmony with the environment. Success in this area is a fundamental condition for ensuring the formal coherence and harmony of urban ensembles. It should be noted that the cities that appear to us to be very coherent have a very large unity of scale. »
The city and architecture must be thought of as a multiple fractal structure. A fractal vision makes it possible to free town planning from a defined scale, because a fractal exists at all scales. Urban processes and mechanisms act at different scales. The notion of events serving at all scales and cooperating across different scales facilitates the understanding of the life and growth of cities. Will the cities of the future become fractal (deterministic?) again? To do so, they must draw inspiration from the formal lessons of the cities of the past while integrating new fractal structures adapted to new technologies.
Benoit Mandelbrot wrote about lengths and the example of measuring a coastline between yesterday and today: “A certain degree of accuracy in measuring coastline lengths has become intrinsic. But this “intrinsic” is quite anthropocentric, since it is the size of the largest stones that man can move, or the cement blocks that he likes to pour. The situation was not very different in the past, since the best n to measure the rib was not the size of a mouse or a fly, but that of an adult man. So anthropocentrism was already intervening, albeit in a different way: somehow the seemingly harmless concept of geographical length is not entirely “objective”, and it never has been. In its definition, the observer inevitably intervenes”. The fractal is the instrument and the measure, the tool and the measure merge.
3-1-1 Form and interpretations of the fractal dimension
This chapter is like the non-exhaustive dissertation, if I do not develop all the terms contrast, symmetry, balance, proportion, scale, matter, character, ornament, texture, colour, ground treatment, harmony…25, there are some that I would like to emphasize in particular conjunction with our subject of study.
Fractal composition can be found in several fields: the city, architecture, music. The feeling of connection to the environment begins with the smallest scales, whose composition determines the impact of the whole. Surface details form the first perceived information and the one through which we connect to the world through a series of successive amplifications. In architecture, it is the ornament at all scales that creates the rhythm. The example of the mosaic walls of the Alhambra which combine extreme flatness due to the support, the interlacing and the play of repetitive patterns, most often geometric, and a certain movement since, when fixing them, one gradually realizes that everything moves, floats, and one is then caught in what Henri Focillon called “metamorphosis”. Metamorphosis participates in the magic of the perception of topological dimensions, spaces change dimensions as in Serge Salat’s installations, where one moves in the fourth dimension.
Ornament is a constant in human history. Ornaments can be traced back to the second millennium B.C.E. in Scotland, where stones have been adorned with spirals that are not unlike certain forms of “Neolithic” Mandelbulbs. The Towie stone is a perfect tetrahedron, representing solid “Platonic” stones nearly 2000 years if not more before their “discovery” by the Greeks…( see Francis Leguen’s excellent article on Neolithic Mandelbulbs, http://www.blog.francis-leguen.com/des-mandelbulbs-neolithiques/ )
Harmony, “A common language specific to the composition is formed which will be a powerful means of unifying the parts. Literally, the unified parts in a composition speak and respond to each other [ … ]. When an urban place, when the architectures that border it, the free spaces that connect it, the lights that pass through it, have reached these correspondences, when we feel a dialogue between the different parts, when each speaks and receives answers, a sacred harmony. It is then that we are attracted by this place, that it awakens our interest, that it gives us emotions, that it requires our intelligence. “It is a light in the negativity of the world.” says Henri Gaudin beautifully about such a place.
Character is a more difficult notion to grasp. It reflects the fact that a composition, by means of its categories, contrasts, balance, scale, form, material, play of light and shadow, must express the destination, the social and symbolic use of the space. It is through character that forms become both identifiable and susceptible to multiple appropriation and use.
The character of a form is peculiar to its geometric and mathematical characteristics. With fractals, we see the emergence of an autonomy of forms that detach themselves from the conditions of their production to acquire a transhistorical value. This is the ultimate meaning of composition: not only to represent the world, but also to understand and compose it to the measure of man.
3-2 Geo-metries and fractals
“In the hands of the Greeks, “geo-metry” gave birth to mathematical geometry. However (as it happens very often in the development of sciences!) mathematical geometry very quickly forgot its origins, having barely scratched the surface of the initial problem “26
Fractal geometry differs from Euclidean geometry by its definition on the one hand: the figures of Euclidean geometry are generally determined by algebraic relations, whereas fractal curves are defined recursively as mentioned above.
We have strayed too far from the original meaning: “All this marvellous structure that comes directly from nature does not appear in the architecture of our century. Something fundamental has been lost, not only do I hope to apply mathematics to architecture and urban planning. I even think it is impossible to make progress without such an application. 27»
“On the subject of the Euclidean order and the fractal order, Perrin 1913 makes two separate remarks about the geometry of nature. On the one hand it is misrepresented by the perfect order of the usual Euclidean forms or differential calculus. On the other hand, it can make one think of the complication of mathematics created around 1900”. Also geometry and the perception of the world are special cases of the fractal dimension.
“Fractal geometry is characterized by two choices: the choice of problems within nature, because to describe everything would be a hopeless and uninteresting ambition, and the choice of tools within mathematics, because looking for applications in mathematics, simply because they are beautiful, has never caused setbacks. Gradually matured, these two choices have created something new: Between the realm of uncontrolled disorder and Euclid’s excessive order, there is now a new zone of fractal order.”
If architecture is full of fractals, can we recognize them, can we establish rules to understand how man with his Euclidean geometry was or was not invaded by fractal geometry?
And if the perception of man by his senses has involved the use of Euclidean forms, then perhaps the much more relative reality involves other forms of perception.
3-3 Rules, grammar and fractal compositions
After the decomposition of the “universal” model comes the controlled phase of recomposition using a grammar that takes into account the constraints of context in the code and thus articulates code and context to produce meaning. The classical rules of fractals, by iterations, juxtaposition, intersection, generate symmetries, asymmetries, and contribute to mark a style. In our study, the recomposition grammar will find the geometric forms of fractals as invariant at the architectural scale, and the fractals themselves as initiator at the urbanistic scale.
In the passage from structure (the code) to discourse (the project), the architect will use different rules depending on the context. The project then responds by covariance in an adequate way to the dimensions of the context. Applied to town planning, our fractal model will be able to follow Nikos Salingaros’s rules28 for the distribution of component sizes, as well as Pareto’s law on structural optimization29( It is, in fact, a hyperbolic distribution). The application of fractals to the urban morphology optimizes it, it is also the case for the uses and functions in a building as well as in the city.30
In addition, there are a number of operations that do not influence internal homothety and that make it possible to generalize the mode of construction. Thus rotations, reflections, the translation of certain elements, a stochastic variation of the reduction factor are allowed within a certain margin.
The challenge for the architect is to undo complexity (decompose) in order to remain in control thanks to the rules (where the economist operates a reduction of complexity) to recompose (re-complexify) in a given context.
3-4 Realism of the architecture generation process
The use of fractals in architecture, and more particularly Mandebulbs, generates a number of paradoxes that it is fair to present.
Concerning the passage from the limit between infinity and finite,31: “To sum up, the physicist is right to treat the passage to the mathematical limit with caution. The fractal dimension implies such a passage, therefore is suspect. I can’t count the number of times a physicist or engineer has pointed this out to me. Perhaps it is because of this suspicion that the physical role of the fractal dimension was not discovered before my own work. But we see that, in this case, the application of the infinitesimal to the finite should not cause any fear if it proceeds with caution.”
The passage from the infinitesimal to the finite thus implies the paradox of the loss of iteration. That is to say that whatever happens, fractal parameterization, as a mathematical tool, gives infinite scales to the created objects, and obviously architecture will, like nature, have to return to a number of iterations consistent with the environment and current techniques. The complexity of the shapes will always be limited by the technique, but the result will nevertheless approach a certain perfection, and will keep the general properties of the fractals we are interested in. At certain scales, fractalization ceases, iteration no longer operates. If one defines different scales that correspond to iterations, the iteration can be selectively interrupted by the architect and the deterministic dimension becomes obsolete because each iteration may have its own rules.
Then, all the algorithms that generate fractals are not deterministic, so we place ourselves in a specific domain that does not always take into account the notions of weighting and randomness, of decomposition and drawing at each new iteration.
Finally, the place of the designer as well as the societal variants will never allow to find a unique formula that will solve all the questions of architecture.
Conclusion
“Computational intelligence must not be content to write programs that substitute for human intelligence to provide automata, which would kill the very soul of architecture. It must enable a human agent to increase the three major areas of his thinking, i.e. his ability to produce reasoning, his ability to imagine and his ability to remember.
This is why it is necessary to develop and test prototypes, each one constituting a palette of tools specific to an architecture, adequate to architectural knowledge and design processes, and to equip them with drawing instruments enriched with concepts (and their multiple semantics), to articulate them to a structure (digital database) allowing a designer to produce his own reasoning, making his way through a semantic network rich in a common history. Such prototypes show how computer science can truly stimulate and amplify invention, understood as the ability to imagine new reasoning based on a memory of the past.
The invention of new concepts will thus in turn feed the design of new tools, capable of supporting new reasoning, in order to meet the expectations of a world in perpetual quest for meaning. In the future, they will thus develop further work on the relationship between topology and geometry, with ontologies describing architectural knowledge at their interface. It will not only be a question of producing tools made up of concepts, but also of reasoning within the framework of know-how. “32
So I tried to show that it is possible to extend the conception of fractal architecture in n dimensions, and to try to apprehend a new tool: the deterministic fractals that are the Mandelbulb, Mandelbox and all other forms resulting from the extension of the Mandelbrot and Julia set. It is conceivable to create an architecture based on deterministic fractals, following the rules and warnings developed during the presentation. History has continuously used natural fractals and fractal objects from iterated function systems. It would now be possible, thanks to new technologies, to use deterministic fractal parameterization in n dimensions for architecture.
Finally, it is at the limit of classical Euclidean geometry and contemporary reasoning on the perception of the world that the concepts set out in this project are to be found. Emmanuelle P. Jeanneret wrote an article a few years ago on the semiotics of the cosmos at the oikos33. It shows the parallel existing between the conception of the space of the cosmos in the great periods of architecture and architectural design. “A possible use of Mandelbrot’s geometry, in its more sophisticated 3D version to produce architecture, seems very interesting to me in that it could offer a new way of integrating the most recent knowledge about the universe into the design of objects that are the supports of our existence. Fractal geometry allows an understanding of the world in n dimensions; this geometry could be seen as the framework of a giant ecosystem, housing subsystems, some of which could be our cities and houses “34. I strongly advise to read Brian Green’s “The Magic of the Cosmos” which tells the whole history of cosmology up to modern theories which are not without recalling the relative character of space-time and the probable fractal dimension of the universe.
These new ways of perceiving the world are reminiscent of the infinite universe of fractals and the perspective of an all-encompassing vision defended by Mandelbrot in an era where everything tends to be divided, cut up and put away in boxes. The perception of our world is probably only a tiny one to which man has access. I therefore defend in my turn a process of perception that seeks at all levels, from the infinitely small to the largest, to ask the question of the coherence of matter on scales of perception that are most often beyond us and whose profound rules we can barely understand.
Lexicon
Fractal: adj. Intuitive sense. A geometric figure or natural object that combines the following characteristics. A) Its parts have the same shape or structure as the whole, except that they are at a different scale and may be slightly distorted. B) Its shape is either extremely irregular or extremely interrupted or fragmented, whatever the scale of examination. C) It contains “distinguishing features” whose scales are very varied and cover a wide range.
Note. The masculine plural is fractals, modelled on navals in preference to fractals.
Statement of requirements. Mathematicians had been dealing for a hundred years with some of the sets in question, but they had not built any theory around them. They had therefore not felt the need for a term to designate them.
Fractal: feminine noun. Mathematical set or fractal physical object.
Fractal dimension: feminine noun. Generic meaning. A number that quantifies the degree of irregularity and fragmentation of a geometric set or natural object, and which is reduced, in the case of objects of the usual Euclidian geometry, to their usual dimension. Specific meaning. “Fractal dimension” has often been applied to the dimension of Hausdorff and Besicovitch, but this use is now strongly discouraged.
“More specifically, once any fractal concept of dimension has been defined, giving the value D, one can try to define a fractal set as being either a set for which D is a non-integer real, or a set for which D is an integer, but the whole is “irregular”. For example we would call fractal a set which gives D=1, but which is not a continuous curve which can be rectified. This would be unfortunate, because the theory of rectifiability is too confusing to depend on it. Moreover it is often possible, by disturbing a very classical set in the vicinity of a single point, to make its dimension become a fraction. From a practical point of view, such examples would be unbearable.”
Fractal set: masculine noun. Replaces fractal when it must be specified that it is a mathematical set.
Fractalist: Amateur of fractals, e.g. researcher or regular user.
Fractal object: masculine noun . Replaces fractal when it must be specified that it is a natural object. A natural object that it is reasonable and useful to represent mathematically by a fractal.
Julia’s sets: are the sets of points in the complex plane. Given two complex numbers, c and Z0, let us define the sequence (Zn) by the recurring relation : Zn+1 = Zn2+ c. There is a different set for each value of C and thus an infinity of Julia’s sets. They are essentially characterized by the fact that a small perturbation at the beginning is reflected in a radical change of this sequence, which will be known later as the “butterfly effect” discovered by the meteorologist Lorentz. Therefore, by taking Z0 = 0 and varying the value of C (real and imaginary part), different shapes are obtained. Thus, a very simple process can give rise, after a large number of iterations, to a very complex shape often resembling species found in nature.
A quaternion: is a type of hypercomplex number. The set of quaternions, constitutes an extension of the set of complex numbers, extension similar to that which had led from the set of real numbers to that of complex numbers. Quaternions were shaped in the nineteenth century, by Hamilton who sought to build a set of numbers having, in space, properties similar to those possessed by complex numbers in the plane. He presents them as quadruplets of real numbers. The set of quaternions can be provided with an addition and a multiplication which makes it one of the first examples of left field . The relation which exists between quaternions and rotations in dimension 3 makes the set of quaternions a useful tool for the treatment of space as in computer graphics or in control theory.
Determinism: masculine noun. 1(Informatics) Quality of systems, processes whose outcome depends only on initial conditions. 2(Philosophy) System according to which natural phenomena are inevitably produced by a necessary sequence of antecedents and consequences, causes and effects. 3(Philosophy) System that denies the influence of free will on human acts.
Appendix 1
A universal distribution law by Nikos Salingaros35
Nikos Salingaros demonstrated a universal rule for the size distribution of urban elements and their multiplicity. In his analysis, scale consists of all elements of approximately the same size. For example, the leaves of a tree belong to the same scale, like the doors in a building.
Ladders should be connected from the smallest to the largest. The analysis presupposes the existence of distinct and consistent levels of scale. If there are too many levels of scale, the environment becomes chaotic. What should be the scale factor, the magnification factor between successive scales? According to Nikos Salingaros, this factor should be between 2 and 5. A factor below 2 fails to create sufficiently distinct scales. A factor greater than 5 prevents the scales from being linked together.
If the scales are separated by factors that are too large, a coherent whole cannot be formed by gradually moving from one scale to another. The inhabitants then no longer feel connected to their environment. In order to achieve coherence of the whole, the elements of the same scale must be linked together and the scales must be linked to each other.
How is this phenomenon mathematically expressed? Very simply by an inverse power law. In a concrete way, how many components of the city must measure the size x? For example, how many streets should there be of width x? If the city is a fractal, the answer is simple. “There are p units of size x, where p is inversely proportional to x”. This means that the smaller the components, the more numerous they must be. The distribution of elements and connections in a living organism (including a living city) thus follows, according to Nikos Salingaros, an inverse power law characteristic of structures with invariance of scale. There must be few large components, a few intermediate-sized components, and a very large number of small ones. A mosque is an example of this inverse power law of scale: large components, full or empty, are few in number (courtyard, iwans, minaret); medium-sized components punctuate space and polarize it (fountains); the rich network of decorative interlacing that makes surfaces vibrate, the muqarnas, the perforations of the moucharabiehs create an almost infinite number of very small elements.
The law of distribution involves separating scales by making them identifiable. This implies an improved structuring of large-scale urbanized regions using permeable but identifiable boundaries, readable in the sense of Kevin Lynch. This structuring is the opposite of contemporary amorphous sururbia. It is in line with the oldest foundation plans.
Nikos Salingaros emphasizes that the hierarchy must continue towards smaller scales (buildings, public spaces, gardens).
This conceptual approach unifies urban planning, urban space design and architecture as the different scales of a single discipline. The most revolutionary aspect of this theory is that it reveals that the distribution of built structures is based on the smallest scales by demonstrating the error of the modernist bias in favour of larger scales.
Structural Entropy, Information and Scale Hierarchy36
The power law for size and frequency distribution is fundamental because it is related to the entropy of the urban system and to information theory. The power law makes it possible to optimize the impact, or relative weight of each structural scale. To quantify the contribution of the scales, Nikos Salingaros uses the physical concept of entropy S. The question raised is the choice of appropriate values of the set of multiplicities p of the different scales.
According to Nikos Salingaros, the inverse power law implies that the smaller scales are closely related to the larger ones, and that one cannot be changed without profoundly altering the other. In other words, changes at any scale propagate entropically, affecting the viewer’s overall perception of the structure.
Entropy then transfers itself by being distributed proportionally over all scales of a complex fractal structure. Structural entropy is additive. The total impact is the sum of the impacts at each scale. The more scales a city or building has, the more entropy (i.e. information) it creates. Subdividing a shape generates structural entropy, and therefore information. In a complex, organized and balanced system, the different scales must have the same entropy so that perception is invariant by changing scale.
« Le potentiel de connectivité d’un tissu urbain est crucial pour son caractère vivant. Une ville physiquement très connectée favorise le mouvement et l’interaction des hommes. L’exemple du centre romain de Turin montre que les îlots complexes résultants de l’évolution sur 2000 ans de la trame romaine ont à la fois la meilleure résilience (ils ont traversé le Moyen-âge, l’Age baroque, la période industrielle), le meilleur potentiel humain (avec 56 km de façades extérieures et intérieures sur une surface de moins de 56 ha) et la meilleure connectivité. »37
Appendix 2
Looking for a beautiful 3D Mandelbrot by Rudy Rucker
Background
The Mandelbrot set M is defined in terms of a mandelmap plane [z,c] which takes z as z*z + c. We add the plane points by adding their cartesian components. This is easy. The multiplication of plane points (in particular the calculation of z times z) is done by pretending that the plane points represent complex numbers. One problem in defining a set of 3D Mandelbrot is that there is no good 3D analogue of complex numbers, and therefore there is no obvious better way to “grid” a 3D point (x, y, z).
Various other ideas have been tried to find the platonic 3D bulb, such as the use of quaternions. The quaternion approach results in starfruit-like structures that do not have the smooth, warty quality we are looking for. Daniel White talks about the quest and some of the approaches in his web page. What do we want? A “Mandelbulb”, a root-like object that is like a large sphere with a dimple in the bottom and bulbs on it, and more warts on the bulbs.
The cubic connectivity map
I will mention here as an aside a completely different approach to the search for a 3D Mandelbrot game. The idea is to take a 3D cross-section of a 4D fractal called Cubic Connectedness Map, which was first studied by Adrian Douady, John Hubbard and John Milnor.
In short, if k is a complex number, we define Mk as the set of complex numbers c such that k and -k, when connected to z, lead to a finely large sequence of iterations in the map z = z^3 – 3*k*z + c. The set of all Mk in k-c space forms the four-dimensional Cubic Connectedness Map or CCM. By incrementing the k parameters from top to bottom, I had the impression that by “stacking” some of these 2D slices while varying a single parameter in real number, like the real part of k, we could obtain a nice 3D mandelote, and I still can’t believe that this is not true. But Paul Nylander recently made a run that seems discouraging.
I still have a slight hope that Paul’s rendering algorithm is not quite what we want, or that we may need to do something more than just stacking 2D sections to find the Mandelbulb in the CCM.
A spherical coordinate algorithm
Another way of thinking about the multiplication of complex numbers is to express (x,y) in polar coordinates (norm,theta). In these coordinates, multiplying two complex numbers means adding their norm values and adding their theta values. This method is easily generalizable to traditional 3D spherical coordinates. A point can be represented by a triple (norm,theta,phi), where phi is the azimuthal elevation above the xy plane, and theta is the polar theta of the projection of the point on the xy plane. And then multiplying two of these numbers means multiplying their norm values, adding their theta, and adding their phis.
Thus, the squaring of a complex number in the plane changes from (r, theta) to (r*r, 2 theta). And in spherical 3D coordinates, (r, theta, phi) becomes (r*r, 2 theta, 2 phi). An encouraging thing in this approach is that we can be sure that the set we get will have a familiar Mandelbrot set like its intersections with the xy plane and the xz plane, because in the xy plane, phi is identically equal to zero; and in the zy plane, theta is identically equal to zero.
White’s algorithm
In 2007, a similar approach was used by Daniel White, who posted about his search for a nice 3D Mandelbort shape on his website. White uses the world “Mandelbulb”, although he’s not sure who first used the word. White’s method of “squaring” a point (x, y, z) is shown below. Note that it’s in C language, where atan2 (y, x) is the arc tangent of y/x, expressed in radians, and trying to evaluate atan2 (0.0, 0.0) crashes the program. White’s method of squaring seems much like mine, I think he’s adding those multiples of pi because he measures phi from the z axis rather than from the xy-plane as I was doing.
double pi = 3.14159265;
double r = sqrt (x*x + y*y + z*z );
double phi = atan2 (sqrt (x*x + y*y) , z ) ;
double theta = atan2 (y , x);
newx = (r*r) * sin ( phi*2 + 0.5*pi ) * cos (theta*2 + pi); newy = (r*r) * sin ( phi*2 + 0.5*pi ) * sin (theta*2 + pi); newz = (r*r) * cos ( phi*2 + 0.5*pi)
Paul Nylander blogged about “hypercomplex fractals”
A guy who call himself Karl131058 pointed out on fractalforum that we can simplify White’s algorithm as follows, with an initial condition to avoid dividing by zero in the main three formulae at the end (without this condition all the points run away and you get an empty set). The point is that you don’t really need to look at the arctan of an angle if you’re planning to take the sine or cosine of it, and even if you’re doubling the angle, you can use the angle doubling formulae cos(2a)=cos^2 a – sin^ a and sin(2a)=2cos a sin a.
Higher-Degree White’s Algorithm
Reasoning by analogy, Daniel White proposed that we look at higher-degree versions of the argument-azimuth approach. He uses this formula for raising a vector to the power n:
He converts (x, y, z) into (r, theta, phi) as before r=sqrt(x²+y²+z²)
theta=atan(y/x)
phi=atan(z/sqrt(x²+y²))
And then he computes (x, y, z) to the n_th power as newx = r^n * cos(n*theta)cos(n*phi)
newy = r^n * sin(n*theta)cos(n*phi)
newz = r^n * -sin(n*phi))
I’m not sure what he does to avoid problems along the z-axis, where x and y are both zero, I suppose he just sets phi equal to the sign of z times pi over 2 there. More information about this approach can be found on the Fractal Forums discussion page.
Why Doesn’t the Argument-Azimuth 3d Mandelbrot Fully Work?
Although we get some good images One problem might be that there’ s some asymmetry in how we get the two angles theta and phi in the spherical coordinates, in that theta is an argument angle the xy plane and the other is an azimuth elevation above it. So maybe it’ s not surprising that simply doubling those angles doesn’t produce a smooth bulbous 3D Mandelbulb. It would be nice if the angles were more similar in origin. Another problem could be that, when we double two angles we’re in some sense moving the point too violently. Perhaps you should be multiplying the angles not by two, but by some weighting factors mul1 and mul2 which might depend on whether, say the point is closer to the xy plane or to the xz plane.
A Two – Azimuth Version
One idea is to define both angles as azimuths like phi. An alternate idea, which I look at in the next subsection, is to define both angles as arguments like theta. For the two – azimuth version, we let phi can be the elevation above the xy plane as before, and now we sup- pose that eta is the azimuth above, say, xz plane. If the point lies in the xy plane, note that theta and eta are the same, for in the xy plane, the xznorm is the same as x. But if the point is off the xy plane then they’ re different. In converting from (r, eta, phi) to (x, y, z), note that xznorm = r cos (eta); xynorm = r cos (phi); xznorm*xznorm + y*y = r*r; and xynorm*xynorm + z*z = r*r
So I build a 3 D Mandelbrot algorithm as before, again not worrying initially about making the rules fast. To distinguish this from my initial “sc” approach in this notebook, I write “taz” in front of the function names, such as tazsquare, tazmandelmap and tazmandel.
This doesn’t seem to work as I continue tweaking the code below, I seem to get blank graphical boxes which suggests that maybe all the points run away to infinity under this iteration and we don’t get any set. Probably I need to be checking for division by zero somewhere. It would be a good idea to convert this into x, y, z form and get rid of the angles and then see what I really have.
A Two – Argument Version
So now let’s try something that’s perhaps more natural than using two azimuths. What if we use two argument- style angles.
Maybe we’ll use the same angle theta that measures the angle between the xy projection and the x axis in the xy plane. And we’ll use a new angle that we’ll call the nuphi, which measures the angle between the xz projection and the x axis in the xz lane. And then we view a 3D point as a triple (r, theta, nuphi), and we’ll square it by passing to (r*r, 2 theta, 2 nuphi). As with the spherical coordinates approach, we can again be sure that the set we get will have a familiar Mandelbrot set as its intersections with both the xy plane and the xz plane.
In principle, this coordinate system should work, as specifying the theta puts the point on a certain plane perpendicular to the xy axis, and specifying the nuphi puts the point in a plane perpendicular to the xz axis, so we have a line as the intersection of these two planes, and the r coordinate picks the point.
Bibliographie
FRANKHAUSER, Pierre (1994) La fractalité des structures urbaines. Paris, Anthropos et Economica.
FRANKHAUSER, Pierre (1991) Aspects fractals des structures urbaines. L’Espace Géographique, n° 1, pp. 45-70.
FRANKHAUSER, Pierre et GENRE-GRANDPIERRE, Cyril (1998) La géométrie fractale, un nouvel outil pour évaluer le rôle de la morphologie des réseaux de transport public dans l’organisation spatiale des agglomérations. Les cahiers scientifiques du transport, n° 33, pp. 41-78.
FRANKHAUSER, Pierre (2003) Morphologie des villes émergentes en Europe à travers les analyses fractales. Besançon, Théma-Puca, Ministère de l’Equipement.
LONGLEY, Paul (2000) Fractal analysis of digital spatial data. Dans Stan Openshaw et Robert.
MANDELBROT, Benoît (1977) The fractal geometry of nature. San Francisco, Freeman.
MANDELBROT, Benoît (2004) Interview, Le Monde 2, 16-17 mai 2004, pp. 60-64.
PELLEGRINO-JEANNERET, Emmanuelle, (2010) Une sémiotique du cosmos à l’oikos ou une architecture du savoir, ELSA Vol II-1-2.
PELLEGRINO-JEANNERET, Emmanuelle, (2011) Introduction ELSA volume III.
SALAT, Serge (2006) Cities and Forms – On Sustainable Urbanism.
TERZIDIS, Kostas (2011) Designing inside the Chinese room, ELSA Vol II-1-2.
Sites consacrés à Mandelbrot :
(http://mandelbrotset.net/tutorial1.html)
(http://pascale.et.vincent.bourges.pagesperso-orange.fr/fractales%20et%20chaos1/index.htm)
Blogs d’informations :
(http://www.blog.francis-leguen.com/des-mandelbulbs-neolithiques/)
(http://urbanmorphologylab.com/)
SALAT, Serge (September 24, 2011) Beyond the Vision artwork exhibition in Beijing,
(http://www.anti-utopias.com/serge-salat-beyond-the-vision/)
[1] Emanuelle Pellegrino-Janneret introduction ELSA volume III
[2] Emanuelle Pellegrino-Janneret introduction ELSA volume III
[3] Cette forme a besoin d’être traduite et comprise à l’aide d’un langage que l’architecte produit. L’ architecte doit contrôler et structurer le discours architectural avec le langage qu’il sous-entend. La position qu’il prend est non déterministe. L’architecte prend position «de manière» non déterministe, quant l’architecture qu’il produit est basée sur une méthode déterministe dans le cas du paramétrage fractal qui nous intéresse. En effet celui-ci s’articule autour des propriétés intrinsèques des fractales déterministes; il est naturel, intuitif, auto-suffisant, auto-générateur. A l’architecte de déterminer le code (déterministe à la base), qui intégrera un certain degré stochastique pour devenir un langage architectural.
[4] MANDELBROT, Benoît (1977) The fractal geometry of nature. San Francisco, Freeman.
[5] Batty et Longley, 1986
[6] Frankhauser, 1994, La fractalité des structures urbaines. Pierre Frankhauser continue la recherche typo-morphologique fractale sur la ville ThéMA (Theory and models for urban and regional planning)
[7] Département d’architecture de l’université Polytechnique de Catalogne en Mars 2003
[8] L’ordre fractal classique p. 339 SALAT, Serge (2011) Cities and Forms – On Sustainable Urbanism.
[9] (Illustration 111.1)
[10] (www.anti-utopias.com/serge-salat-beyond-the-vision/)
[11] (Illustration 111.2)
[12] Jean-Pierre Kahane Professeur à l’Université Paris Sud, Orsay Membre de l’Académie des Sciences
[13] Je mets les liens pour une annexe 2 qui sera facultative mais très utile à celui qui veut.
[14] (Illustration 12.1)
[15] (voir définition lexique)
[16] -cf : La ville fractale, chapitre 2, partie 1, page 53, SALAT, Serge (2006) Cities and Forms – On Sustainable Urbanism.
[17] http://www.fractalforums.com/tutorials/mandelbulb3d-tutorial-list/
[18] (Francis Le Guen – avril 01, 2013)
[19](Illustration 23.1)
[20] (Illustration 23.2)
[21] (Illustration 23.3)
[22] (Illustration 23.4)(Illustration 23.5)
[23] (Illustration 23.6)
[24] http://www.blog.francis-leguen.com/des-mandelbulbs-neolithiques/ http://nms.scran.ac.uk/database/record.php?usi=000-100-033-206-C
[25] cf : chapitre 3, partie 1, page 332, SALAT, Serge (2006) Cities and Forms – On Sustainable Urbanism.
[26] Benoit Mandelbrot
[27] Nikos Salingaros
[28] -cf : chapitre 3, partie 1, page 66, SALAT, Serge (2006) Cities and Forms – On Sustainable Urbanism.
[29] -cf : chapitre 5, partie 3 page 475, SALAT, Serge (2006) Cities and Forms – On Sustainable Urbanism.
[30] -cf : chapitre 3, page 177 , page 209,, SALAT, Serge (2006) Cities and Forms – On Sustainable Urbanism.
[31] Benoit Mandelbrot
[32] Emanuelle Pellegrino-Janneret introduction ELSA volume III
[33] E. P. Jeanneret, Une sémiotique du cosmos à l’oikos ou une arhitecture du savoir, ELSA Vol 2-1-2 2010.
[34] E. P. Jeanneret Apport de synthèse après entrevue
[35] SALAT, Serge (2006) Cities and Forms – On Sustainable Urbanism.
[36] SALAT, Serge (2006) Cities and Forms – On Sustainable Urbanism.
[37] Serge (2006) Cities and Forms – On Sustainable Urbanism. Page 49 La connectivité et la fractalité.
ont contribués à la réalisation de ce mémoire
Pierre Pellegrino
Directeur de mémoire
Emmanuelle P. Jeanneret
Docteur en architecture
Francis Le Guen
Fractaliste, journaliste, explorateur
Serge Salat
Directeur du laboratoire des morphologies urbaines
Novembre 2013